Effective Area
When solving the problem of eccentrically loaded foundations the program offers two options to deal with an affective dimension of the foundation area:
- a rectangular shape of the effective area is assumed
- general shape of the effective area is assumed
Rectangular shape
A simplified solution is used in such cases. In the case of axial eccentricity (bending moment acts in one plane only) the analysis assumes a uniform distribution of contact stress σ applied only over a portion of the foundation l1, which is less by twice the eccentricity e compared to the total length l.
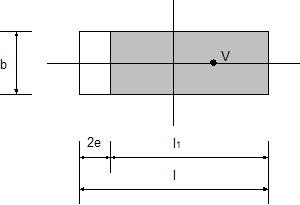 Determination of effective area in case of axial eccentricity
Determination of effective area in case of axial eccentricity
An effective area (b*l1) is assumed to compute the contact stress so that we have:
![]()
In case of a general eccentric load (foundation is loaded by the vertical force V and by bending moments M1 and M2 the load is replaced by a single force with given eccentricities:
![]()
![]()
The size of affective area follows from the condition that the force V must act eccentrically:
![]()
General shape of contact stress
In the case of an eccentric load the effective area is determined from the assumption that the resultant force V must act in the center of gravity of the compressive area. The theoretically correct solution appears in Fig.
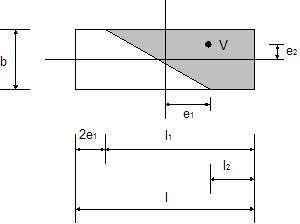 Determination of contact stress for general eccentricity - general shape
Determination of contact stress for general eccentricity - general shape
Owing to considerable complexity in determining the exact location of the neutral axis, which in turn is decisive when computing the effective area, the program follows the solution proposed by Highter a Anders1), where the effective areas are derived with the help of graphs.
1) Highter, W.H. - Anders,J.C.: Dimensioning Footings Subjected to Eccentric Loads Journal of Geotechnical Engineering. ASCE, Vol. 111, No GT5, pp 659 - 665.